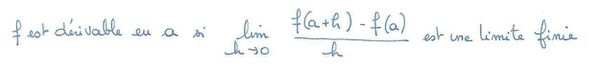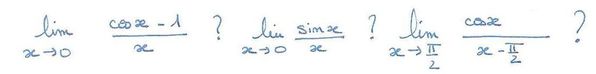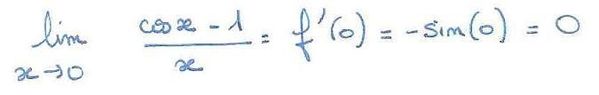Overblog
Suivre ce blog Administration + Créer mon blog
24 septembre 2010 5 24 /09 /septembre /2010 12:40

T°S : La Continuité

Souvent étudiée en début d'année, la continuité est une notion nouvelle pour les élèves de T°S.

 

A quoi ca sert ? 

A montrer qu'une fonction est continue.

 

Oui, mais à quoi ça sert de montrer qu'une fonction est continue?

A en calculer la primitive ( vous apprendrez à faire cela un peu plus tard).

Et calculer la primitive d'une fonction permet ensuite de calculer des aires sur un graphique... ben voila!

 

On fait ça comment?

Pour montrer que f est continue en une valeur a, on utilise le théorème qui dit :

 

  fconti1

 

Oui, mais concrètement ça donne quoi?

Visuellement, une fonction est continue si on peut tracer sa courbe sans lever le stylo. Mais vous imaginez bien que ce n'est en aucun cas une justification valable sur une copie! 

Premièrement, une fonction qui n'est pas définie en certaines valeurs, ne sera pas continue en ces valeurs.

Donc f non définie en a => f non continue en a

 

Ensuite, certaines fonctions sont définies en une valeur mais n'y sont pas continues, ce sont des fonctions un peu bizarres que vous n'avez jamais vues auparavant, et que vous ne verrez plus beaucoup cette année. Mais elles sont très utiles pour travailler et s'exercer sur le chapitre continuité!

    Premier exemple :

conti1 

On dit qu'on a prolongé f (qui n'est pas définie en 0 au premier abord) par continuité en 0, en lui donnant la valeur 1.

Montrons que f est continue en 0: 

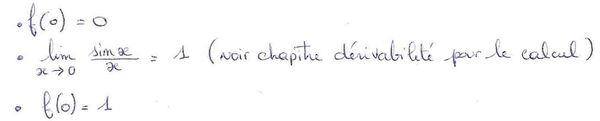
conti2

  On peut  donc écrire l'égalité :

conti3  

Conclusion, f est bien continue en 0.

     Deuxième exemple :

  conti4

Montrons qu'elle n'est pas définie en 2 par exemple : 

conti5

La fonction admet 2 limites différentes en 2, donc elle n'est pas continue en 2.

 

Une propriété importante, sujet de ROC :

f dérivable en a   =>  f continue en a

Mais le contraire est FAUX. 

Cette propriété constitue une ROC, dont voici le schéma de démonstration :

 

CLE de démonstration :    Soit f dérivable en a, alors

fderi4

J'effectue un produit en croix :

conti7

Si je passe à la limite en a de chaque côté :

conti8

Or

conti9

Donc

conti10

On retrouve le théorème de continuité.

 

Pour plus de détails dans les explications, ou pour un cours sur ce chapitre ou d'autres, contactez moi : lesbonnesnotes@yahoo.fr

Partager cet article
Repost0
Published by Joséphine - dans Maths T°S
commenter cet article …
23 septembre 2010 4 23 /09 /septembre /2010 21:16

T°S : Dérivabilité

L'année commence fort avec un chapitre très théorique, sur la dérivabilité (rappels de 1°S) et la continuité ( nouveauté).

Comme à chaque fois, posons nous les bonnes questions, et commençons par...

 

  • la dérivabilité

 

A quoi ca sert ?    A montrer qu'une fonction est dérivable.

 

Oui, mais à quoi ça sert de montrer qu'une fonction est dérivable?   A la dériver. Et dériver une fonction permet ensuite d'étudier ses variations.. ben voila!

 

On fait ça comment?   Là, on se réfère à la page sur les dérivées en 1°S

 

Et pourquoi on étudie la dérivabilité dans le chapitre des limites ?

Il y a 2 façons d'utiliser le théorème :

- pour montrer qu'une fonction est dérivable en a, avec la 1ère formule :  

fderii1

- pour calculer la limite d'une fonction quand x tend vers a, avec la 2ième formule : 

fderi3

  fderi2

 

Expliquons cette deuxième notion: 

Si on sait que f est dérivable en a, on peut donc écrire directement l'égalité:

fderi4

Cette égalité donne la valeur de la limite d'une expression en x. Cela veut dire que l'on peut utiliser le théorème pour calculer certaines limites, comme par exemple les 3 ci-dessous, souvent posées en devoir surveillé : 

fderi5

 

La méthode    

Comment savoir qu'il faut utiliser le théorème de dérivabilité?

Par élimination!!

Quelles sont les différentes méthodes pour calculer une limite?

  • le calcul direct ( ici on obtient une forme indéterminée),
  • le théorème du terme de plus haut degré, mais qui ne s'applique qu'en l'infini ET pour des polynomes ou frations rationnelles ( pas le cas ici),
  • la forme conjuguée, le plus souvent valable pour les racine.

 

On vient d'éliminer toutes les méthodes, ne reste plus que le théorème de dérivabilité.

 

Calculons la limite du 1er exemple : 

On doit comparer la 2ième formule du théorème à notre expression.

On voit que a = 0   (limite en 0)   et    f(x) = cos(x)

 

Vérifions le reste :   x - a = x - 0 = x, c'est ok

f(a) = f(0) = cos (0) = 1, c'est ok.

 

On peut donc écrire :

fderi6

 Or, cos(x) est dérivable sur IR, donc en 0. Je peux donc affirmer, d'après le théorème, que

  fderi7

( on rappelle que la dérivée de cos(x) est  -sin(x) )

 

 

Entraînez vous sur le même schéma à faire les 2 autres limites, et en cas de problème, contactez moi par email !

 

 

Partager cet article
Repost0
Published by Joséphine - dans Maths T°S
commenter cet article …