Résolutions graphiques de fonctions en T°ES (et T°S)

L'étude des fonctions a un caractère spécifique en section économique. On ne vous demande pas de connaître la théorie mais on contraire, de maîtriser parfaitement les méthodes graphiques et les applications au monde réel.

Les méthodes calculatoires, lorsqu'on vous donne l'expression de f(x), ce qu'il faut savoir, et savoir faire :

- dériver une fonction, donc connaître le tableau des dérivées.
- trouver les variations d'une fonction, donc savoir étudier le signe d'une expression en x (f'),
- trouver l'équation d'une tangente, donc connaître la formule de la tangente en x=a,
- calculer des limites, et donc connaître le tableau de calculs et les formes indéterminées,
- donner les équations des asymptotes,
- démontrer qu'une droite est asymptote oblique à une courbe, et donc connaître son théorème,
- calculer la position relative d'une droite par rapport à une courbe.

Les méthodes graphiques, lorsque vous n'avez pas l'expression de f(x) mais vous avez sa courbe, ce qu'il faut savoir, et savoir faire :

- trouver l'image d'une valeur de x par f, trouver la valeur d'un antécédent,
- trouver f'(12) ou f'(-5), c'est à dire savoir calculer le coefficient directeur de la tangente en 12 ou en -5,
- savoir faire un tableau de variations en lisant le graphique,
- savoir résoudre des équations (f(x) = 3) ou des inéquations (f(x) > 5) sur f,
- savoir résoudre des équations (f'(x) = 3) ou des inéquations (f'(x) > 0) sur f' (et donc connaître la signification graphique du signe ou de la valeur de f'),
- savoir donner les variations de la fonction composée de f et d'une fonction usuelle (par exemple les variations de 1/f(x)) , donc connaître les théorèmes sur les variations de fonctions composées.

Nous allons ici détailler ces méthodes graphiques.

Exemple 1 : Soit le graphique suivant, - Cf est en rouge, et des droites sont en vert, bleu et noir.

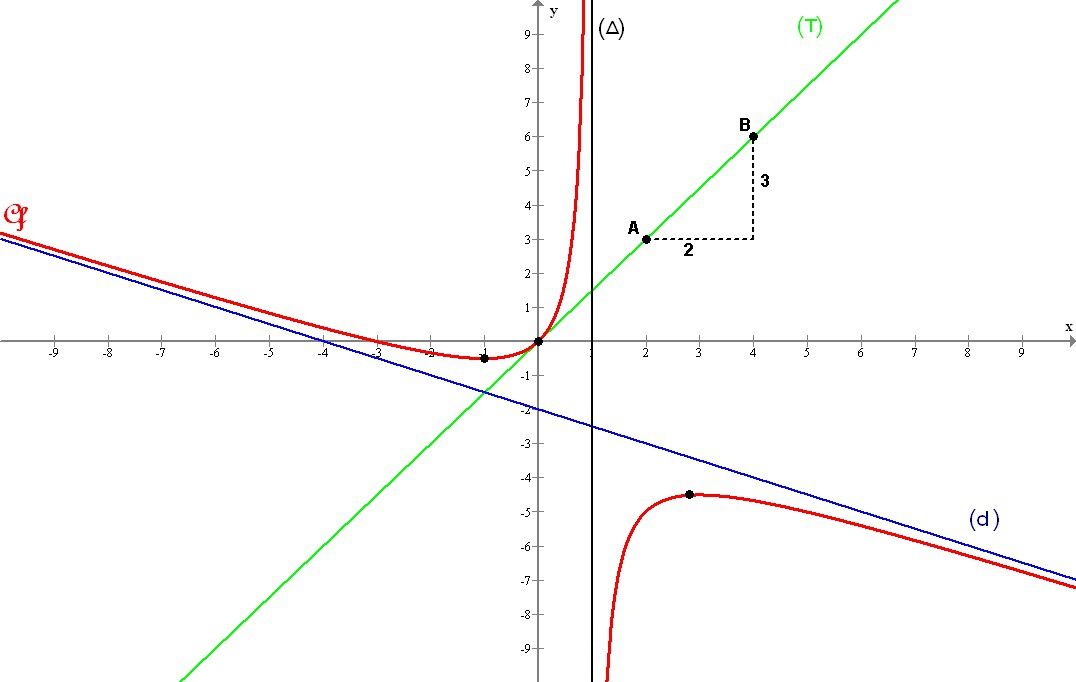
1) Donner les valeurs de f(-3) et f(4)
Il faut donner l'image par f de -3 et de 4, donc donner l'ordonnée des points de la courbe d'abcisses -3 et 4. On trouve donc f(-3) = 0 et f(4) = -5.

2) Donner la valeur de f'(0)
Que représente la dérivée graphiquement? C'est le coefficient directeur de la tangente au point considéré. Donc f'(0) est le coefficient directeur de (T) en vert.
Méthode pour calculer graphiquement le coef directeur d'une droite : on repère 2 points de coordonnées entières sur (T), et on compte le nombre de carreaux que l'on suit pour aller du 1er point au second. Le coef directeur est alors égal au nombre de carreaux verticaux divisé par le nombre de carreaux horizontaux ( attentionx aux signes : si je descends, on met un "-", si je monte, on met un "+").
Application : ici pour aller de A vers B, je traverse 2 carreaux vers la droite et 3 vers le haut, donc le coef directeur vaut 3/2, d'où f'(0)=3/2. 

3) Donner les valeurs de f'(-1) et f'(2,8)
Comme précédemment, f'(-1) et f'(2,8) sont les coefficients directeurs des tangentes en -1 et 2,8. Mais ici les tangentes ne sont pas dessinées, et on ne peut le faire soi-même. Il faut donc se demander ce qu'il se passe en -1 et 2,8. En ces points, la courbe change de variation, ce qui signifie que ce sont des valeurs où la dérivée est nulle! Donc f'(-1) = 0 et f'(2,8) = 0.

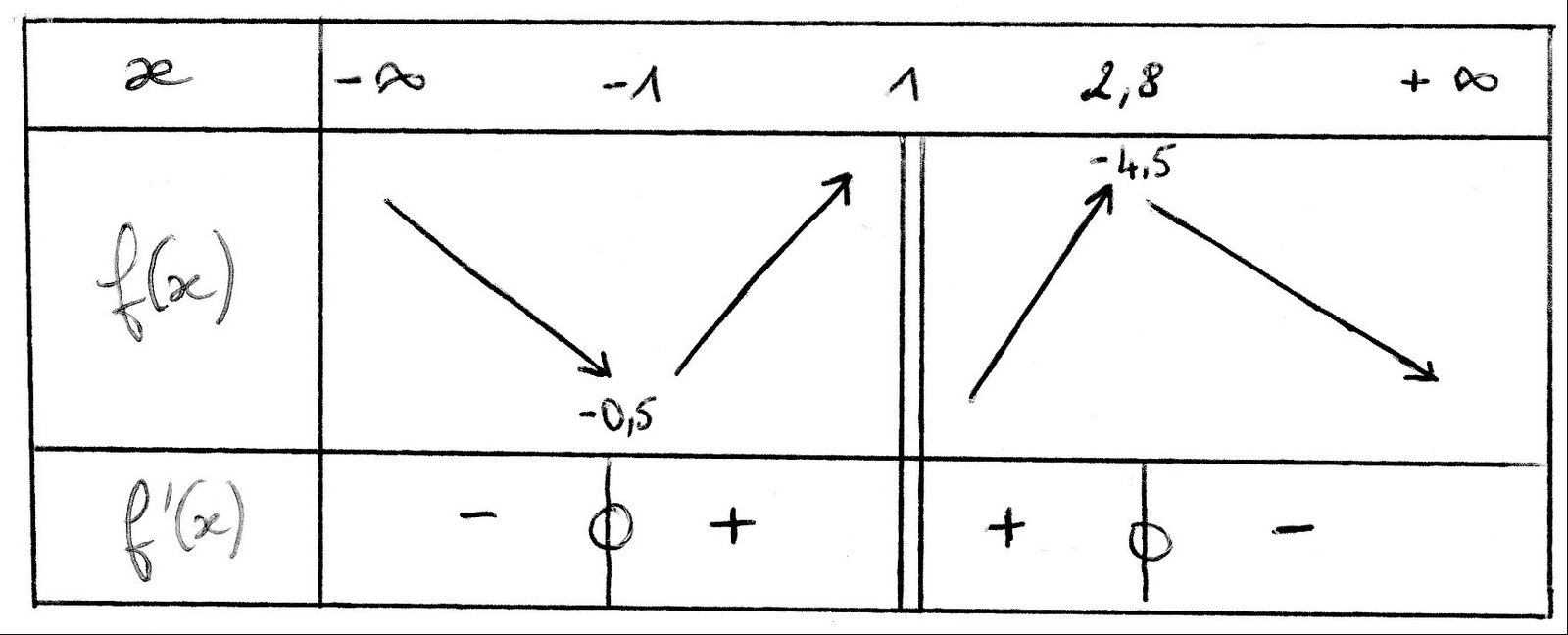
4) Etablir le tableau de variations de f et en déduire le signe de f'
Il comportera 2 lignes, la ligne pour x et la ligne pour f(x) avec les flèches. Que doit-on inscrire sur la ligne de x ?
- aux 2 extrémités, les bornes de l'intervalle d'etude, ici - ∞ et + ∞,
- puis la ou les valeurs interdites s'il y en a. Ce sont des valeurs de x par lesquelles Cf ne passe pas, ici c'est x= 1,
- enfin les valeurs de x pour lesquelle la courbe change de variations, ici en -1 et en 2,8.

5) Donner les équations des asymptotes à Cf
- Cf ne traverse pas Δ, elle n'a pas de valeur en x=1. Donc la droite Δ d'équation x=1 est asymptote verticale à Cf.
- Cf se rapproche de (d) en bleue, quand x tend vers +/- ∞. Donc (d) est une asymptote oblique à Cf. Pour trouver son équation, du type y=ax+b, il suffit de trouver graphiquement son coefficient directeur "a" et son ordonnée à l'origine "b". Pour trouver "a", (d) passe par (-4,0) et (0,-2). donc a = -2 / 4 = -0,5. Son ordonnée à l'origine vaut -2. Donc (d) a pour équation y = -0,5x - 2 (pour plus de détails sur ces méthodes voir là).

Exemple 2 : Soit le graphique suivant, - Cf est en rouge, et des droites sont en vert & bleu.

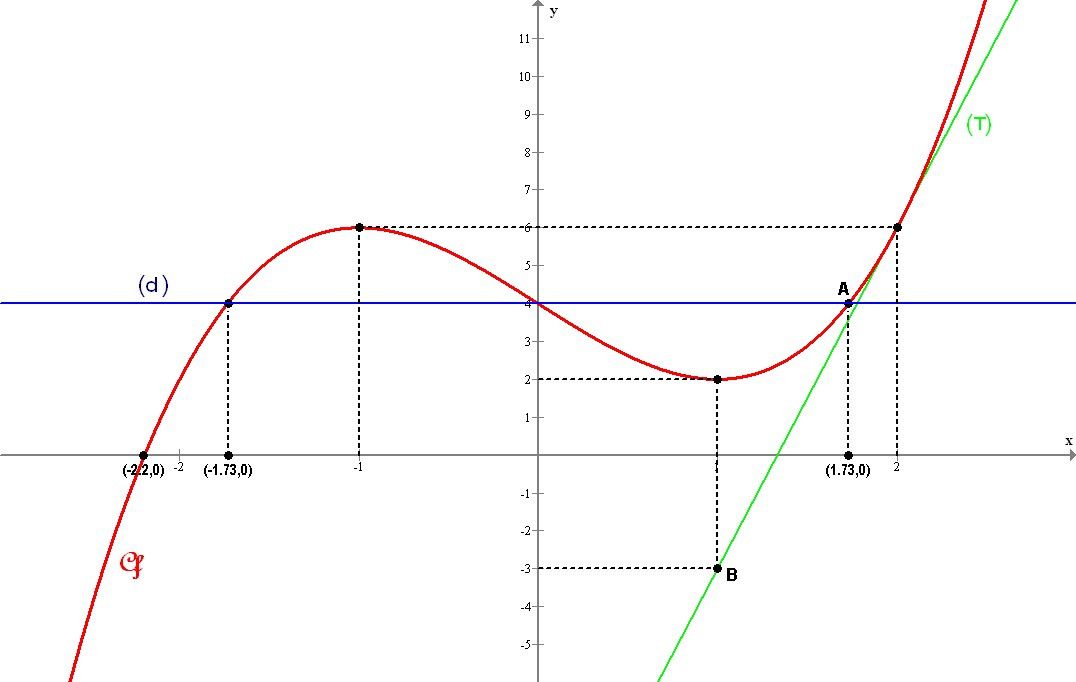
1) Résoudre graphiquement f(x) = 4
Méthode : on trace la droite d'équation y=4 (droite horizontale), et les solutions de l'équation f(x) = 4 sont les abcisses ( donc les x) des points où cette droite coupe la courbe. Ici les solutions sont S = {-1,73, 0  , 1,73}.

2) Résoudre graphiquement f'(x) = 0
Graphiquement, que signifie que f' est nulle? Cela signifie que f change de variation, qu'il y a un extremum. Donc ici, ce sont les abcisses des points où f change de variation, soit S = {-1 , 1}.

3) Résoudre graphiquement f(x) < 4
Méthode : on trace la droite d'équation y=4 (droite horizontale), et les solutions de l'inéquation f(x) < 4 sont les intervalles de x où la courbe est en dessous de la droite ( les valeurs de ses y sont inférieures à 4). Ici les solutions sont S = ]- ∞ , -1,73[ U ]0, 1,73[.

4) Résoudre f(x) > 0
On reprend la méthode précédente en utilisant directement l'axe des abcisses ( y=0). Les solutions sont les intervalles de x où la courbe est au dessus de cet axe. Ici S =  ]-2,2, +∞[

5) Résoudre f'(x) > 0
Graphiquement , que signifie "f' est positive"? Cela signifie que la courbe Cf est croissante. Donc les solutions sont les intervalles de x où f est croissante, soit S=]- ∞ , -1[ U ]1, + ∞[.

6) Etablir les variations de g(x) = 1 / f(x)
la fonction g(x) = 1 / f(x) est la composée de 1/X et de f(x). D'après les cours sur les fonctions composées (là), et en sachant que 1/f(x) n'est définie que lorsque f(x) ≠ 0 et que 1/x est toujours décroissante, alors:

- g(x) sera définie sur ]- ∞ , -2,2[ U ]2,2 , + ∞[,
- sur ]- ∞ , -2,2[ U ]-2,2 ,-1[ U ]-1, + ∞[, f(x) est croissante et 1/x est décroissante, donc g(x) est décroissante.
- sur ]-1, 1[, f(x) est décroissante et 1/x est décroissante, donc g(x) est croissante.

Pour vérifier que vous avez compris, entraînez-vous, et répondez aux questions suivantes :
1er graphique :
- Résoudre f'(x) = 0
- Résoudre f'(x) > 0
- Résoudre f(x) < 0
- Etablir les variations de 1/f(x)
2ie graphique:
- Dresser le tableau de variations de f
- Donner les antécédents de 5
- Donner les valeurs de f'(1) et f'(2).

Pour un entraînement efficace, pour vérifier que vous avez compris le chapitre et pour vous préparer au prochain contrôle, faites appel à mes services de cours par correspondance... Renseignez-vous    ICI.